Rumus Bangun Ruang / Dimensi Tiga

Bangun Ruang / Dimensi Tiga | Selamat datang di matematrick. Kali ini kita akan membahas tentang materi matematika yang cukup mengasyikkan dan menantang, yaitu bab Dimensi Tiga / Bangun Ruang.
Materi bangun ruang sendiri sebenarnya sudah pernah saya tuliskan di postingan tentang Jaring-Jaring Kubus, Balok, Prisma, dan Limas. Lalu, untuk sekarang apa sajakah yang akan kita pelajari? Diantaranya adalah tentang : Sifat-sifat kubus, balok, prisma, limas, tabung, kerucut dan bola. Mari kita bahas satu per satu.

1. Sifat dan Rumus-rumus Kubus

Kubus merupakan bangun ruang tiga dimensi yang dibatasi oleh enam bidang sisi yang kongruen/ sama berbentuk persegi.

Sifat-sifat Kubus

1. Memiliki 6 buah sisi berbentuk persegi (bujur sangkar)
   (ABCD, EFGH, ABFE, CDHG, ADHE dan BCGF)
2. Memiliki 12 rusuk yang sama panjang
   (AB,BC,CD,DA,EF,FG,GH,HE,EA,FB,HD,GC)
3. Memiliki 8 titik sudut yang sama besar (siku-siku)
   (∠A, ∠B, ∠C, ∠D, ∠E, ∠F, ∠G, ∠H)
4. Mempunyai 12 diagonal bidang yang sama panjang
   (AC, BD,EG,HF,AF,EB,CH,DG,AH,ED,BG,CF)
5. Mempunyai 4 diagonal ruang
   (AG,BH,CE,DF)

 Bentuk Kubus

AB = Sisi / Rusuk
BE = Diagonal Bidang
AG = Diagonal Ruang

Contoh Jaring-jaring Kubus

Rumus Volume dan Luas Permukaan Kubus

Volume   = sisi x sisi x sisi = s3
Luas     = 6 x sisi x sisi    = 6s2
Keliling = 12 x s
Diagonal bidang = s√2
Diagonal ruang  = s√3

2. Sifat dan Rumus-rumus Balok

Balok adalah bangun ruang yang terdiri dari enam sisi berbentuk persegi panjang dengan dua diantaranya berukuran berbeda. Balok dapat kita aplikasikan kedalam kehidupan sehari-hari, seperti almari, kulkas, kotak amal dan lain-lain.

Sifat-sifat Balok

1. Memiliki 6 buah sisi yang terdiri dari 3 pasang sisi yang besarnya sama
   (ABCD dengan EFGH, EFGH dengan ABCD, ADHE dengan BCGF)
2. Memiliki 12 rusuk yang terdiri dari 3 keleompok rusuk-rusuk yang sama
   dan sejajar
   AB = CD = EF = GH = panjang
   BC = FG = AD = EH = lebar
   AE = BF = CG = DH = tinggi
3. Memiliki 8 titik sudut
   (∠A, ∠B, ∠C, ∠D, ∠E, ∠F, ∠G, ∠H)
4. Mempunyai 12 diagonal bidang
   (AC, BD,EG,HF,AF,EB,CH,DG,AH,ED,BG,CF)
5. Mempunyai 4 diagonal ruang yang sama panjang
   (AG,BH,CE,DF)

Bentuk gambar balok dan contoh jaring-jaring balok.

AF = BG = Diagonal Bidang
AG = Diagonal Ruang

Beberapa Contoh Jaring Jaring Balok

Rumus Volume dan Luas Permukaan Balok

Volume          = p x l x t
Luas            = 2 x { (p x l ) + (p x t) + (l x t) }
Keliling        = 4 x (p + l + t )
Diagonal ruang  = √p2+ √l2 + √t2
Diagonal Bidang = √s2+ √s2

3. Macam, Unsur, Volume dan Luas Permukaan Prisma

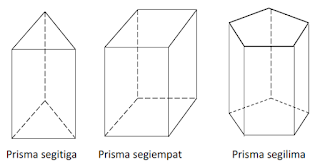
 Prisma adalah bangun ruang yang dibatasi oleh dua buah bidang berbentuk segi banyak yang sejajar dan sisi-sisi tegak yang berpotongan menurut rusuk-rusuk yang sejajar.

Macam - macam Prisma

1. Prisma Segitiga
2. Prisma Segiempat
3. Prisma Segi-n

Unsur-unsur dalam Prisma Segi-n

1. Jumlah titik sudut = 2n
2. Jumlah bidang = n + 2
3. Jumlah rusuk = 3n
4. Jumlah diagonal bidang = n(n+1)
5. Jumlah diagonal ruang = n(n-3)

Rumus Volume dan luas permukaan Prisma

Volume = Luas alas x tinggi
Luas Permukaan = ( 2 x luas alas) + jumlah luas sisi tegak

4. Unsur, Rumus Volume dan Luas Permukaan Limas

Limas adalah bangun ruang yang dibatasi oleh alas berbentuk segi-n yang kemudian dari sisi alas tersebut dibentuk sisi tegak berbentuk segitiga dan bertemu pada satu titik puncak.

Gambar macam-macam Limas

Unsur Limas Segi-n

1. Jumlah titik sudut = n + 1
2. Jumlah bidang = n + 1
3. Jumlah rusuk = 2n
4. Jumlah diagonal bidang = n/2(n - 3)
5. Tidak memiliki diagonal ruang

Rumus Volume dan Luas Permukaan Limas

Volume = 1/3 x Luas alas x tinggi
Luas Permukaan = luas alas + jumlah luas sisi tegak

5. Sifat, Rumus, dan Jaring Tabung
Tabung adalah bangun ruang berbentuk prisma tegak beraturan dengan alas dan tutupnya berupa lingkaran.

Sifat-sifat Tabung

1. Mempunyai 3 bidang sisi : alas, tutup dan selimut (sisi tegak)
2. Bidang alas dan tutup berupa lingkaran
3. Sisi tegak berupa bidang lengkung yang dinamakan selimut tabung
4. Mempunyai 2 rusuk : rusuk alas dan tutup
5. Tinggi tabung: jarak titik pusat alas dan titik pusat tutup
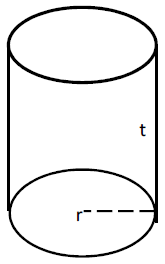
6. Jari-jari lingkaran alas dan tutup besarnya sama

Gambar Tabung

Jaring-jaring Tabung

Rumus Volume dan luas permukaan Tabung

Luas alas = luas tutup = luas lingkaran = πr2
Luas selimut tabung    = 2πrt
Luas permukaan tabung  = 2 x luas alas + luas selimut
                       = 2 πr2 + 2πrt
                       = 2πr(r + t)
Volume tabung = luas alas x tinggi
              = πr2t

Itulah lima buah bangun ruang dimensi tiga mulai dari kubus, balok, prisma, limas dan tabung meliputi sifat-sifatnya, gambar, jaring-jaring, sampai rumus menentukan volume dan luas permukaannya. Untuk rumus-rumus bangun ruang lainnya seperti kerucut, bola, dan lain-lainnya yang belum tercantum di atas akan kita bahas di lain kesempatan.
Terima kasih sudah membaca postingan tentang rumus-rumus bangun ruang dimensi tiga ini, semoga ada manfaat yang bisa didapat. Sukses untuk Anda semua . Salam hangat.

Dapatkan artikel terbaru: