Cara Cepat Menentukan KPK dan FPB

Cara Cepat Menentukan KPK dan FPB | Selamat datang para pecinta matematika. Kali ini kita akan belajar pelaran yang mudah sekali, yaitu cara menentukan KPK dan FPB dari beberapa bilangan.

1. Cara Cepat Menentukan FPB

FPB adalah Faktor Persekutuan Terbesar dari 2 bilangan atau lebih. Faktor artinya ‘pembagi’. Maka FPB berarti sebuah angka terbesar yang dapat membagi 2 bilangan atau lebih sekaligus.

Misalnya bilangan 18 dan 24, maka FPB – nya adalah 6 dimana 18 : 6 = 3 dan 24 : 6 = 4.

Ada banyak cara menentukan FPB.
Pertama, dengan cara menentukan faktor (pembagi) kedua bilangan tersebut :

Faktor dari 18 adalah : 1 x 18
2 x 9
3 x 6
( 1, 2, 3, 6, 9, dan 18)

Faktor dari 24 adalah : 1 x 24
2 x 12
3 x 8
4 x 6
( 1, 2, 3, 4, 6, 8, 12, dan 24 )

Faktor-faktor yang bersekutu adalah : 1, 2, 3, dan 6
Faktor persekutuan terbesar (FPB) nya adalah 6


Teknik Kedua menentukan FPB : dengan cara TABEL

Faktor	18	24
2	9	12
2	9	6
2	9	3
3	3	1
3	1	1

Faktor 2 dapat membagi bilangan 18 dan 24 sekaligus,

Faktor 3 dapat membagi bilangan 9 dan 3 sekaligus,

Maka FPB adalah 2 x 3 = 6

Teknik Ketiga, dengan cara Faktorisasi Prima / Pohon Faktor :

            

Teknik Keempat, dengan cara cepat

Selisihkan kedua bilangan tersebut : 24 : 18 = 6

FPB = 6

Contoh 1

Tentukan FPB dari 72 dan 90 !

Jawab :

Contoh 2:

Tentukan FPB dari 20 dan 60 !

Jawab :

Contoh 3:

Tentukan FPB dari 25 dan 45!

Jawab :

2. Cara Cepat Menentukan KPK

KPK adalah Kelipatan Persekutuan Terkecil dari 2 bilangan atau lebih. Kelipatan artinya hasil perkalian bilangan tersebut dengan bilangan rasional. Maka KPK berarti sebuah angka terkecil hasil perkalian 2 bilangan atau lebih.

Misalnya bilangan 6 dan 8, maka KPK – nya adalah 24 dimana 6 x 4 = 24 dan 8 x 3 = 24

Ada banyak cara menentukan KPK.

Teknik Pertama, dengan cara menentukan persekutuan kelipatan kedua bilangan tersebut :
Kelipatan 6 adalah : 6, 12, 18, 24, 30… dan seterusnya
Kelipatan 8 adalah : 8, 16, 24, 32, … dan seterusnya
Kelipatan persekutuannya adalah : 24, 48, 72, . . . dan seterusnya
Kelipatan Persekutuan Terkecil – nya (KPK) adalah 24

Teknik Kedua, dengan cara metode sisir (TABEL):

Faktor	6	8
2	3	4
2	3	2
2	3	1
3	1	1

Kelipatan Persekutuannya adalah 2 x 2 x 2 x 3 = 24 (angka pada lajur kiri di kalikan semua)

Teknik Ketiga, dengan cara Faktorisasi Prima / Pohon Faktor :

            

Keempat, dengan cara cepat

Tentukan KPK dari 6 dan 8!

Jawab:

Ambil bilangan terbesar yaitu 8

Kelipatan 8 = 8, 16, 24, . . .

Bagilah dengan bilangan lain setiap kelipatan mulai dari   8  (8 : 6 = …) bukan . . .

                                                                                           16. (16 : 6 = …) bukan . . .

                                                                                           24  (24 : 6 = 4) ya . . .

KPK = 24

Contoh :

Tentukan KPK dari 4 , 8,  dan 10 !

Jawab :

Bilangan terbesar = 10

Kelipatan 10 = 10, 20, 30, 40, . . .

10 : 4 … bukan

20 : 4 = 5 , tapi 20 : 8 = bukan

30 : 4 = bukan,

40 : 4 = 10 dan 40 : 8 = 5, ya …

Jadi KPK = 40

   

Kumpulan Contoh Soal dan Pembahasan KPK dan FPB

Contoh Soal dan Penyelesaian Cara Menentukan KPK

Contoh Soal 1:

Sari dan Mila mengikuti les piano ditempat yang sama. Sari latihan setiap 6 hari sekali , Mila latihan setiap 4 hari sekali. Jika hari ini mereka les bersama, berapa hari lagi mereka les bersama kembali?

Penyelesaian:

Diketahui : Sari les 6 hari sekali dan Mila les 4 hari sekali

Ditanya     : KPK dari 6 dan 4

Jawab       : 6 = 2 X 3

      4 = 2 X 2 = 2²

      KPK dari 6 dan 4 = 2² X 3 = 4 X 3 = 12

Jadi mereka les bersama kembali 12 hari kemudian.

Contoh Soal 2:

Terdapat 2 buah lonceng. Lonceng pertama berbunyi setiap 15 menit sekali, lonceng kedua berbunyi setiap 12 menit sekali. Tiap berapa menit lonceng menyala bersama?

Penyelesaian:

Diketahui : Lonceng pertama berbunyi 15 menit sekali dan Lonceng kedua berbunyi 12 menit sekali

Ditanya     : KPK dari 15 dan 12

Jawab      

15 = 3 X 5

12 = 2 X 2 X 3 = 2² X 3

KPK dari 15 dan 12 = 2² X 3 X 5 = 60

Jadi kedua lonceng menyala bersama setiap 60 menit sekali, atau satu jam sekali

Contoh Soal 3:

Bu Santi belanja ke pasar setiap 8 hari sekali, sedangkan Bu Rita belanja setiap 6 hari sekali. Pada tanggal 7 Juli 2015 mereka berbelanja bersama. Pada tanggal berapa mereka berbelanja bersama lagi?

Penyelesaian:

Diketahui : Bu Santi ke Pasar setiap 8 hari sekali, Bu Rita setiap 6 hari sekali.

Ditanya     : KPK dari 8 dan 6

Jawab       : 8 = 2 X 2 x 2 = 2³

      6 = 2 X 3

         KPK dari 8 dan 6 = 2³ X 3 = 9 X 3 = 24

Mereka berbelanja setiap 24 hari sekali dan bertemu pada 7 juli 2015.

7  + 24 = 31

Jadi mereka berbelanja bersama lagi pada tanggal 31 juli 2015

Contoh Soal 4:

Lampu A menyala setiap 40 detik. Lampu B menyala setiap 1 menit. Dalam waktu 15 menit, berapa kali kedua lampu menyala bersama-sama?

Penyelesaian:

Diketahui : Lampu A menyala setiap 40 detik dan Lampu B menyala setiap 1 menit.

Ditanya     : dalam 15 menit berapa kali kedua lampu menyala bersama.

Jawab       : 1 menit = 60 detik

40 = 2 x 2 x 2 x 5 = 2³ x 5

60 = 2 X 2 X 3 X 5 = 2² X 3 X 5

KPK 40 dan 60 adalah = 2³X 3 X 5 = 8 x 3 x 5 = 120

Kedua lampu menyala setiap 120 detik.

15 menit = 900 detik

900 detik : 120 detik = 7,5

Jadi dalam 15 menit kedua lampu menyala bersama sebanyak 7 kali 

Contoh Soal 5:

Deni berenang setiap 8 hari sekali, Andi berenang setiap 2 minggu sekali, dan Tora berenang setiap 6 hari sekali. Setiap berapa hari sekali mereka bertiga berenang bersama?

Penyelesaian:

Diketahui : Deni berenang 8 hari sekali, Andi 14 hari sekali, dan Tora 6 hari sekali

Ditanya     : KPK 8, 14 dan 6 

Jawab       :

8 = 2 X 2 x 2 = 2³

14 = 2 x 7

6 =  2 X 3

KPK 8, 14 dan 6 adalah 2³ x 3 x 7 = 168

Jadi mereka bertiga berenang bersama setiap 168 hari sekali.

Contoh Soal FPB dan Penyelesaiannya Lengkap

Contoh Soal 1:

Pak bayu memiliki 64 buah Apel dan 48 buah jeruk. Kedua buah tersebut akan diagikan kepada temannya sama banyak. Berapa banyak teman Pak Bayu yang dapat menerima kedua buah tersebut ?

Penyelesaian:

Diketahui :     64 apel dan 48 jeruk

Ditanya:         FPB  64 dan 48

64 = 2 x 2 x 2 x 2 x 2 x 2 = 2⁶

48 = 2 x 2 x 2 x 2 x 3 = 2⁴ x 3

FPB dari 64 dan 48 adalah 2⁴ =16

Jadi banyak teman Pak Bayu yang dapat menerima kedua buah tersebut adalah 16 orang.

Contoh Soal 2:

Bu mira akan membuat parsel dari 24 botol sirup, 40 kaleng biskuit dan 72 bungkus cokelat. Bu mira ingin membuat parsel dari bahan-bahan tersebut dengan jenis dan bahan yang sama. Berapa jumlah parsel terbanyak yang dapat dibuat bu Mira?

Penyelesaian:

Diketahui :     24 botol sirup, 40 kaleng biskuit, 72 bungkus cokelat

Ditanya:         FPB  24, 40 dan 72

24 = 2 x 2 x 2 x 3 = 2³ x 3

40 = 2 x 2 x 2 x 5 = 2³ x 5

72 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²

FPB  24, 40 dan 72 adalah 2³ = 8

Jadi jumlah parsel terbanyak yang dapat dibuat bu Mira adalah 8 parsel.

Contoh Soal 3:

Hani memiliki pita merah sepanjang 18 meter, pita biru 54 meter, dan pita kuning 36  meter. Ketiga pita tersebut akan digunakan untuk menghias kotak kado sebanyak-banyaknya dengan panjang dan warna yang sama tiap kotaknya. Berapa jumlah kotak kado terbanyak yang dapat dihias?

Penyelesaian:

Diketahui :  18 meter pita merah, 54 meter pita biru, 36 meter pita kuning. 

Ditanya:      FPB  18, 54, dan 36

18 = 2 x 3 x 3 = 2 x 3²

54 = 2 x 3 x 3 x 3 = 2 x 3²

36 = 2 x 2 x 3 x 3 = 2² x 3²

FPB  18, 54, dan 36 = 2 x 3² = 2 x 9 = 18

Jadi jumlah kotak kado terbanyak yang dapat dihias adalah 18 kotak.

Contoh Soal 4:

Kepada Desa menyediakan bantuan berupa 125 buah buku tulis dan 75 buah pena untuk dibagikan ke anak-anak sebanyak-banyaknya . Tiap anak mendapatkan buku tulis dan pena sama banyak. Berapa pena yang didapatkan oleh tiap anak?

Penyelesaian:

Diketahui :   125 buah pena dan 75 buah pena  . 

Ditanya:       pena yang didapatkan tiap anak

125 = 5 x 5 x 5 = 5³

75  = 3 x 5 x 5 = 3 x 5²

FPB dari 125 dan 75 adalah 5² = 25, jadi ada 25 anak yang mendapatkan bantuan.

Banyak pena yang didapatkan tiap anak yaitu ;

75 : 25 = 3

Jadi banyak pena yang didapatkan oleh tiap anak adalah 3 buah pena.

Contoh Soal 5:

Bu Nani akan mengadakan arisan dirumahnya. Ia membeli sejumlah kue untuk disajikan pada tamu, yaitu 48 buah kue soes, 84 buah kue dadar gulung, 60 buah  kue putu ayu dan 96 buah kue bolu kukus. Kue- kue tersebut akan disajikan di atas piring sebanyak-banyaknya. Berapa jumlah piring yang dibutuhkan untuk menyaikan kue-kue tersebut?

Penyelesaian:

Diketahui :          48 soes, 84 dadar gulung, 60 putu ayu, dan 96  bolu kukus 

Ditanya      :         FPB dari 48, 84, 60 dan 96

48 = 2 x 2 x 2 x 2 x 3 = 2⁴ x 3

84 = 2 X 2 X 3 X 7 = 2² X 3 X 7

60 = 2 X 2 X 3 X 5 = 2² X 3 X 5

96 = 2 X 2 X 2 X 2 X 2 X 3 = 2⁵ X 3

FPB dari 48, 84, 60 dan 96 adalah 2²X 3 = 4 X 3 = 12

Jadi piring yang dibutuhkan untuk menyaikan kue-kue tersebut adalah 12 piring

Contoh Soal Cara Menghitung FPB dengan Faktorisasi Prima

Contoh Soal 1

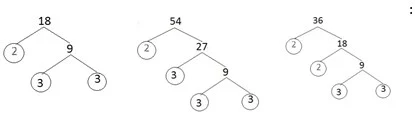
Coba kalian tentukan FPB dari 36, 54, dan 72

Cara Menjawab
Pertama-tama kalian harus melakukan faktorisasi prima terhadap ketiga bilangan yang ada:

36 = 2² × 3²

54 = 2 × 3³

72 = 2³ × 3²

Kita dapat menentukan FPB dari 36, 54, dan 72 dengan cara mengambil bilangan hasil faktorisasi yang nilainya sama kemudian mengalikannya dengan pangkat terendah. Jadi dari soal di atas bilangan pokok yang sama adalah 2 kemudian bilangan berpangkat terendahnya adalah 3² maka FPB dari ketiga bilangan tersebut adalah 2 × 3² = 18

Contoh Soal 2

Tentukan FPB dari 4, 8, dan 12 dengan faktorisasi prima

Cara Menjawab:

Faktorisasi prima dari 4 = 2²

Faktorisasi prima dari 8 = 2³ = 2² x2

Faktorisasi prima dari 12= 2² x 3

Langsung saja kita ambil bilangan berpangkat terendah yang ada pada hasil faktorisasi prima di atas yaitu 2² . Maka dapat disimpulkan bahwa FPB dari 4, 8, dan 12 adalah 2²= 4

Demikianlah penjelasan dan pembahasan yang dapat kami berikan mengenai beberapa Contoh Soal dan Penyelesaian Cara Menentukan KPK Semoga apa yang dijelaskan di atas bisa kalian pahami dengan baik,

Dapatkan artikel terbaru: