Cara Menyelesaikan Persamaan Kuadrat dengan Cepat

Selamat datang di matematrick.com, tempat belajar matematika secara online, mudah dan menyenangkan. Pada kesempatan kali ini kita akan membahas berbagi teknik cara menyelesaikan persamaan kuadrat. Sudah siap? Mari kita mulai.

Penyelesaian Persamaan Kuadrat dengan Pemfaktoran

Dalam menentukan penyelesaian persamaan kuadrat sama halnya dengan menentukan akar-akar persamaannya. Hasil-hasil dari penyelesaian tersebut bisa kita bilang sebagai himpunan penyelesaian atau HP. Secara umum bentuk dari persamaan kuadrat adalah  ax² + bx + c = 0, dimana a ≠0 dan a,b,c € R.

Namun bila kita bicara tentang geometris, dalam menentukan penyelesiaan pesamaan kuadrat berarti menentukan titik-titik potong kurva dengan sumbu X. Cara menentukan himpunan penyelesaian persamaan kuadrat dapat menggunakan tiga cara, yaitu :

1. Memfaktorkan
2. Melengkapkan kuadrat sempurna
3. Rumus kuadrat (rumus abc) 

Penyelesaian Persamaan Kuadrat dengan Memfaktorkan

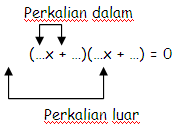
Kita ibaratkan jikalau suatu persamaan kuadrat dapat kita ubah menjadi bentuk AB = 0, maka penyelesaiannya adalah A=0 atau B=0. Dari situ kita bisa tahu bahwa untuk menentukan penyelesaian persamaan kuadrat ax² + bx + c = 0 dengan pemfaktoran yaitu dengan menentukan faktor dari perkailan ac yang jumlahnya adalah b, semisal faktornya adalah r dan s. Sehingga perkalian luar dan perkalian dalam dari koefisien besarnya r dan s. Perhatikan pola berikut !

Contoh soal 1:
Tentukan Himpunan Penyelesaian dari x²– 2x – 8 = 0 !
 Jawab :

 x2 - 2x - 8     = 0
(x - 4) (x + 2)  = 0
     x = 4 dan x = -2    Jadi HP { 4,-2 }

Contoh soal 2:
Tentukan Himpunan Penyelesaian dari 6x² – x – 5 = 0 !

Jawab :

 6x2 - x - 8      = 0
(6x + 5) (x - 1)  = 0
     x = -5/6 dan x = 1    Jadi HP { -5/6,1 }

Berikutnya adlah menyelesaikan persamaan kuadrat dengan cara melengkapkan kuadrat sempurna

Penyelesaian Persamaan Kuadrat dengan Kuadrat Sempurna

Kita tahu ada 3 cara dalam menyelesaikan persamaan kuadrat, yakni pemfaktoran, melengkapkan kuadrat sempurna dan rumus ABC. Dan kali ini saya akan menjelaskan tentang  penyelesaian persamaan kuadrat dengan melengkapkan kuadrat sempurna.

Penyelesaian Persamaan Kuadrat dengan Melengkapkan Kuadrat Sempurna

Penyelesaian dengan cara ini cukup rumit jadi hati-hatilah dalam penyelesaiannya. Dengan metode ini kita akan mengubah bentuk ax²– bx – c = 0 menjadi (x + p)² = q sehingga penyelesaiannya x = -p ± √q . Langkah pertama, ubah menjadi bentuk kemudian menambahkan kedua ruas denganhal ini akan menjadikannya kuadrat sempurna.

Contoh Soal :
Tentukan himpunan penyelesaian dari x² + 13 = 6x

Menentukan Akar Akar Persamaan Kuadrat dengan Rumus ABC

Salah satu teknik menyelesaikan persamaan kuadrat adalah dengan cara rumus ABC. Penyelesaian ini bisa juga dikatakan sebagai metode rumus kuadrat.

Penyelesaian Persamaan Kuadrat dengan Rumus Kuadrat ( Rumus ABC )

Bentuk umum rumus kuadrat adalah dimana b² – 4ac disebut dengan Diskriminan ( D ). jadi D = b² – 4ac. Rumus inilah yang kita gunakan dalam menentukan akar-akar persamaan kuadrat.

Contoh Soal :
Tentukan akar-akar dari persamaan kuadrat 2x² + 3x -9 = 0, ( a=2| b=3| c=-9 )!

Demikianlah materi tentang persamaan kuadrat dan teknik cara menyelesaikan  persamaan kuadrat dengan 3 cara; menfaktorkan, melengkapkan kuadrat sempurna dan menggunakan rumus ABC. Semoga bisa menambah pengertian anda tentang persamaan kuadrat. Salam.

Dapatkan artikel terbaru: