Rumus Segitiga : Mengenal Jenis Segitiga dan Rumusnya
Pengertian Segitiga
Segitiga adalah sebuah bidang datar yang terbentuk oleh tiga buah garis yang saling berpotongan atau sebuah bidang datar yang dibatasi oleh tiga buah garis yang memiliki tiga buah sudut.
Pada suatu bangun datar segitiga, sudut terbesar yang di miliki selalu berhadapan dengan sisi yang mempunyai ukuran terpanjang dan sisi dengan ukuran paling pendek selalu berhadapan dengan sudut yang terkecil. Ini disebut sifat Ketaksamaan Segitiga.
Di lihat dari panjang sisi-sisinya segitiga di bedakan menjadi tiga macam yaitu :
Pada suatu bangun datar segitiga, sudut terbesar yang di miliki selalu berhadapan dengan sisi yang mempunyai ukuran terpanjang dan sisi dengan ukuran paling pendek selalu berhadapan dengan sudut yang terkecil. Ini disebut sifat Ketaksamaan Segitiga.
Jenis-Jenis Segitiga Dilihat Dari Panjang Sisi-Sisinya
Di lihat dari panjang sisi-sisinya segitiga di bedakan menjadi tiga macam yaitu :
a. Segitiga sama sisi
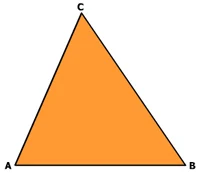
Segitiga sama sisi adalah segitiga yang mempunyai tiga sisi sama panjang dan semua sudutnya sama besarnya yaitu 600.
Perhatikan gambar segitiga sama sisi KLM di atas,
- Panjang KL = LM = KM
- Sudut K = Sudut M = Sudut L ( yaitu 600 )
Sifat-sifat segitiga sama sisi
- Mempunyai tiga buah sumbu simetri putar tingkat tiga serta bisa menempati bingkainya dengan tepat dengan enam cara.
- Mempunyai tiga buah sisi yang sama panjang.
- Mempunyai tiga buah sudut yang sama besar.
b. Segitiga sama kaki
Segitiga sama kaki adalah segitiga dengan dua sisinya yang sama panjang dan terbentuk dari dua segitiga siku-siku yang kongruen.
Perhatikan gambar segitiga sama kaki di atas,
Segitiga sembarang adalah segitiga dengan ketiga sisinya tidak sama panjang dan juga sudut-sudutnya tidak sama besar.
Perhatikan segitiga sembarang ABC di atas ,
Dilihat dari besar sudut-sudutnya jenis segitiga di bedakan dalam tiga jenis yaitu :
a. Segitiga lancip
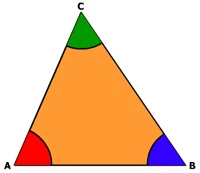
Segitiga yang memiliki tiga buah sudutnya berbentuk lancip dimana besar masing-masing sudutnya lebih dari 00 dan kurang dari 900 disebut dengan segtitiga lancip.
Perhatikan gambar segitiga lancip ABC di atas,
b. Segitiga siku-siku
Segitiga dengan salah satu sudutnya berukuran 900 disebut dengan segitiga siku-siku.
Perhatikan gambar segitiga siku-siku ABC di atas,
c. Segitiga tumpul
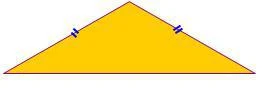
Segitiga yang salah satu sudutnya tumpul dimana salah satu sudutnya lebih dari 900 tetapi kurang dari 1800 di sebut dengan segitiga tumpul.
Perhatikan gambar segitiga tumpul PQR di atas,
Dilihat dari panjang sisi-sisinya dan besar sudut-sudutnya segitiga di bedakan dalam tiga jenis yaitu :
a. Segitiga siku-siku sama kaki
Segitiga yang memiliki besar salah satu sudutnya 900 dan kedua sisinya sama panjang biasa di sebut dengan segitiga siku-siku sama kaki.
b. Segitiga lancip sama kaki
Segitiga dengan sudut lancip dan kedua sisinya sama panjang di sebut dengan segitiga lancip sama kaki.
c. Segitiga tumpul sama kaki
Segitiga yang mempunyai salah satu sudutnya tumpul dan memiliki dua sisi yang sama panjangnya.
Berikutnya kita akan belajar rumus-rumus yang berlaku di dalam segitiga siku siku, segitiga sama kaki, dan segitiga sama sisi.
Segitiga sama kaki adalah segitiga dengan dua sisinya yang sama panjang dan terbentuk dari dua segitiga siku-siku yang kongruen.
Perhatikan gambar segitiga sama kaki di atas,
- Panjang PQ = PR ( PQ dan PR di sebut kaki ).
- Sudut Q = Sudut R ( di sebut sudut-sudut kaki segitiga PQR ).
- Sisi QR merupakan alas dan Sudut P adalah sudut puncak.
Sifat-sifat segitiga sama kaki
- Mempunyai satu buah sumbu simetri dan dapat menempati bingkainya dengan pas dengan dua cara.
- Memiliki dua buah sisi yang sama panjang dan juga memiliki dua buah sudut yang sama besarnya.
c. Segitiga sembarang
Segitiga sembarang adalah segitiga dengan ketiga sisinya tidak sama panjang dan juga sudut-sudutnya tidak sama besar.
Perhatikan segitiga sembarang ABC di atas ,
- Panjang AB ≠ BC ≠ CA.
- sudut A ≠ sudut B ≠ sudut C.
Jenis-Jenis Segitiga Dilihat Dari Besar Sudut-Sudutnya
Dilihat dari besar sudut-sudutnya jenis segitiga di bedakan dalam tiga jenis yaitu :
a. Segitiga lancip
Segitiga yang memiliki tiga buah sudutnya berbentuk lancip dimana besar masing-masing sudutnya lebih dari 00 dan kurang dari 900 disebut dengan segtitiga lancip.
Perhatikan gambar segitiga lancip ABC di atas,
- Sudut A, sudut B dan Sudut C merupakan sudut lancip.
b. Segitiga siku-siku
Segitiga dengan salah satu sudutnya berukuran 900 disebut dengan segitiga siku-siku.
Perhatikan gambar segitiga siku-siku ABC di atas,
- Sudut A merupakan sudut siku-siku yang ukurannya adalah 900.
- Memiliki sisi tegak, sisi datar dan sisi miring.
- Mempunyai sudut siku-siku ( 90° )
- hypotenusa atau sisi miring pada segitiga siku-siku selalu terletak di depan sudut siku-siku.
c. Segitiga tumpul
Segitiga yang salah satu sudutnya tumpul dimana salah satu sudutnya lebih dari 900 tetapi kurang dari 1800 di sebut dengan segitiga tumpul.
Perhatikan gambar segitiga tumpul PQR di atas,
- Sudut P merupakan sudut tumpul dari segitiga tersebut.
Jenis-Jenis Segitiga Dilihat Dari Panjang Sisi-Sisinya Dan Besar Sudut-Sudutnya
Dilihat dari panjang sisi-sisinya dan besar sudut-sudutnya segitiga di bedakan dalam tiga jenis yaitu :
a. Segitiga siku-siku sama kaki
Segitiga yang memiliki besar salah satu sudutnya 900 dan kedua sisinya sama panjang biasa di sebut dengan segitiga siku-siku sama kaki.
b. Segitiga lancip sama kaki
Segitiga dengan sudut lancip dan kedua sisinya sama panjang di sebut dengan segitiga lancip sama kaki.
c. Segitiga tumpul sama kaki
Segitiga yang mempunyai salah satu sudutnya tumpul dan memiliki dua sisi yang sama panjangnya.
Berikutnya kita akan belajar rumus-rumus yang berlaku di dalam segitiga siku siku, segitiga sama kaki, dan segitiga sama sisi.
Rumus Segitiga Siku-siku
Apa itu pengertian segitiga siku-siku
Segitiga siku-siku adalah sebuah segitiga yang salah satu dari tiga sudutnya mempunyai sudut 90⁰ atau siku-siku, seperti yang bisa kamu lihat pada gambar di atas.
Pada gambar diatas pada titik C sudut siki-siku dari segitiga tersebut.
Rumus-rumus segitiga siku-siku
a. Jika panjang sisi a dan panjang sisi b sudah diketahui ukurannya maka panjang sisi c dapat ditentukan dengan persamaan c2= a2 + b2
b. Jika panjang sisi a dan panjang sisi c sudah diketahui ukurannya maka panjang sisi b dapat ditentukan dengan persamaan b2 = c2 – a2
c. Jika panjang sisi b dan panjang sisi c sudah diketahui ukurannya maka panjang sisi a dapat ditentukan dengan persamaan a2 = c2 – b2
Persamaan di atas biasa di sebut dengan teorema phytagoras.
Sedangkan untuk menghitung keliling segitiga siku-siku dapat digunakan rumus :
K = sisi a + sisi b + sisi c, atau
K = sisi + sisi + sisi
Dan untuk luas segitiga siku-siku dapat di gunakan persamaan :
L = ½ x alas x tinggi
L = ½ x a x t
1. Sebuah segitiga PQR adalah segitiga siku-siku dengan sudut siku-sikunya berada di titik P. Hitung panjang QR, jika panjang PQ 8 cm
dan panjang PR 6 cm !
Jawab :
Diketahui :
PQ = 8 cm
PR = 6 cm
Ditanya :
QR . . . . ?
Jawab :
QR2 = PQ2 + PR2
QR2 = 82 + 62
QR2 = 64 + 36
QR2 = 100
QR = 10 cm
Jadi panjang sisi QR adalah 10 cm
2. Perhatikan gambar segitiga di atas , jika panjang sisi c = 13 cm dan panjang sisi a = 5 cm, hitunglah panjang sisi b !
Diketahui :
c = 13 cm
a = 5 cm
ditanya :
b . . . ?
jawab :
b2 = c2 - a2
b2 = 132 – 52
b2 = 169 – 25
b2 = 144
b = 12 cm
jadi panjang sisi b adalah 12 cm
3. Jika diketahui tinggi segitiga 4 cm dan alasnya 6 cm, hitunglah luasnya !
Diketahui :
t = 4 cm
a = 6 cm
ditanya :
L . . . .?
Jawab :
L = ½ x a x t
L = ½ x 6 cm x 4 cm
L = 12 cm2
Jadi luas segitiga adalah 12 cm2
4. Hitunglah keliling segitiga jika panjang sisi-sisinya 5 cm, 3 cm dan 4 cm !
Diketahui :
Misalkan
Sisi a = 5 cm
Sisi b = 4 cm
Sisi c = 3 cm
Ditanya :
K . . . . ?
Jawab :
K = sisi a + sisi b + sisi c
K = 5 cm + 4 cm + 3 cm
K = 12 cm
Jadi keliling segitiga tersebut adalah 12 cm.
 |
| Gambar segitiga siku siku |
Segitiga siku-siku adalah sebuah segitiga yang salah satu dari tiga sudutnya mempunyai sudut 90⁰ atau siku-siku, seperti yang bisa kamu lihat pada gambar di atas.
Pada gambar diatas pada titik C sudut siki-siku dari segitiga tersebut.
Rumus-rumus segitiga siku-siku
a. Jika panjang sisi a dan panjang sisi b sudah diketahui ukurannya maka panjang sisi c dapat ditentukan dengan persamaan c2= a2 + b2
b. Jika panjang sisi a dan panjang sisi c sudah diketahui ukurannya maka panjang sisi b dapat ditentukan dengan persamaan b2 = c2 – a2
c. Jika panjang sisi b dan panjang sisi c sudah diketahui ukurannya maka panjang sisi a dapat ditentukan dengan persamaan a2 = c2 – b2
Persamaan di atas biasa di sebut dengan teorema phytagoras.
Sedangkan untuk menghitung keliling segitiga siku-siku dapat digunakan rumus :
K = sisi a + sisi b + sisi c, atau
K = sisi + sisi + sisi
Dan untuk luas segitiga siku-siku dapat di gunakan persamaan :
L = ½ x alas x tinggi
L = ½ x a x t
Contoh soal segitiga siku-siku dan pembahasannya
1. Sebuah segitiga PQR adalah segitiga siku-siku dengan sudut siku-sikunya berada di titik P. Hitung panjang QR, jika panjang PQ 8 cm
dan panjang PR 6 cm !
Jawab :
Diketahui :
PQ = 8 cm
PR = 6 cm
Ditanya :
QR . . . . ?
Jawab :
QR2 = PQ2 + PR2
QR2 = 82 + 62
QR2 = 64 + 36
QR2 = 100
QR = 10 cm
Jadi panjang sisi QR adalah 10 cm
2. Perhatikan gambar segitiga di atas , jika panjang sisi c = 13 cm dan panjang sisi a = 5 cm, hitunglah panjang sisi b !
Diketahui :
c = 13 cm
a = 5 cm
ditanya :
b . . . ?
jawab :
b2 = c2 - a2
b2 = 132 – 52
b2 = 169 – 25
b2 = 144
b = 12 cm
jadi panjang sisi b adalah 12 cm
3. Jika diketahui tinggi segitiga 4 cm dan alasnya 6 cm, hitunglah luasnya !
Diketahui :
t = 4 cm
a = 6 cm
ditanya :
L . . . .?
Jawab :
L = ½ x a x t
L = ½ x 6 cm x 4 cm
L = 12 cm2
Jadi luas segitiga adalah 12 cm2
4. Hitunglah keliling segitiga jika panjang sisi-sisinya 5 cm, 3 cm dan 4 cm !
Diketahui :
Misalkan
Sisi a = 5 cm
Sisi b = 4 cm
Sisi c = 3 cm
Ditanya :
K . . . . ?
Jawab :
K = sisi a + sisi b + sisi c
K = 5 cm + 4 cm + 3 cm
K = 12 cm
Jadi keliling segitiga tersebut adalah 12 cm.
Rumus Segitiga Sama kaki
Rumus Segitiga Sama kaki - Segitiga sama kaki mempunyai pengertian sebuah segitiga yang mempunyai dua sisi yang sama panjang dan dua sudut yang sama besar yaitu sudut yang berhadapan dengan sisi yang panjangnya sama.
Segitiga sama kaki dibentuk dari 2 buah segitiga siku siku yang kongruen yakni dengan cara menghimpitkan kedua sisi yang panjangnya sama.
Perhatikan gambar di atas. Segitiga ADC dan segitiga BDC adalah 2 buah segitiga siku siku yang kongruen. Sisi CD adalah sisi siku siku yang sama panjangnya dari kedua segitiga siku siku diatas. Jadi bisa kita peroleh kesimpulan bahwa segitiga ABC adalah sebuah segitiga sama kaki dengan sisi AC=BC yang sama panjangnya sebagai kaki dari segitiga tersebut.
Segitiga sama kaki mempunyai sifat-sifat antara lain :
1. Memiliki 2 buah sisi yang sama panjangnya sebagai kaki dari segitiga
2. Memiliki 1 sumbu simetri
3. Memiliki 2 buah sudut yang besarnya sama yakni sudut-sudut yang berhadapan dengan sisi yang sama panjang.
4. Segitiga sama kaki adalah salah satu bangun lipat simetri yang bisa menempati bingkainya dengan dua macam cara.
Segitiga adalah bagian salah satu dari bangun datar yang mempunyai keliling dan
luas.
Untuk menghitung Keliling segitiga sama kaki di gunakan rumus :
K = sisi 1 + sisi 2 +sisi 3
Jadi untuk mencari keliling segitiga sama kaki dengan menjumlahkan semua panjang sisi-sisinya( pada dasarnya hal ini sama dengan semua rumus keliling segitiga )
Untuk menghitung Luas segitiga sama kaki di gunakan rumus :
L = ½ a x t
dimana L adalah luas, a adalah panjang alas dan t adalah tinggi dari segitiga tersebut.
1. Jika di ketahui sebuah segitiga sama kaki panjang alasnya 12 cm sedangkan panjang kakinya 10 cm. Hitunglah luas dan keliling segitiga tersebut !
Jawab :
Diketahui :
a = 12 cm
s = 10 cm
ditanya :
a. K . . . . ?
b. L . . . . ?
Jawab :
a. Keliling segitiga
K= sisi 1 + sisi 2 + sisi 3
K = 12 cm+ 10 cm + 10 cm
K = 32 cm
b. Luas segitiga
Coba kamu perhatikan gambar segitiga segitiga sama kaki di bawah ini.

aC adalah tinggi segitiga, untuk mencari tinggi sebuah segitiga siku-siku kita bisa menggunakan persamaan phytagoras. Jika alasnya adalah 12 cm maka panjang aB = 6 cm
aC2 = BC2 - aB2
aC2 = 102 – 62
aC2 = 100 – 36
aC2 = 64
aC = 8 cm
jadi tinggi segitiga tersebut = 8 cm
Luas segitiga = ½ x a x t
L = ½ x 12 x 8
L = 48 cm2
Jadi keliling segitiga sama kaki tersebut 32 cm sedangkan luanya 48 cm2.
2. Jika diketahui luas segitiga 48 cm2. Hitung tinggi segitiga jika alasnya 12 cm !
Diketahui :
L = 48 cm2
a = 12 cm
ditanya :
t . . . . ?
jawab :
L = ½ x a x t
48 = ½ x 12 x t
48/0,5 = 12 x t
96 = 12 x t
96/12 = t
8 cm = t
Jadi tinggi segitiga tersebut 8 cm.
Segitiga sama kaki dibentuk dari 2 buah segitiga siku siku yang kongruen yakni dengan cara menghimpitkan kedua sisi yang panjangnya sama.
 |
| gambar segitiga sama kaki |
Segitiga sama kaki mempunyai sifat-sifat antara lain :
1. Memiliki 2 buah sisi yang sama panjangnya sebagai kaki dari segitiga
2. Memiliki 1 sumbu simetri
3. Memiliki 2 buah sudut yang besarnya sama yakni sudut-sudut yang berhadapan dengan sisi yang sama panjang.
4. Segitiga sama kaki adalah salah satu bangun lipat simetri yang bisa menempati bingkainya dengan dua macam cara.
Rumus segitiga sama kaki
Segitiga adalah bagian salah satu dari bangun datar yang mempunyai keliling dan
luas.
Untuk menghitung Keliling segitiga sama kaki di gunakan rumus :
K = sisi 1 + sisi 2 +sisi 3
Jadi untuk mencari keliling segitiga sama kaki dengan menjumlahkan semua panjang sisi-sisinya( pada dasarnya hal ini sama dengan semua rumus keliling segitiga )
Untuk menghitung Luas segitiga sama kaki di gunakan rumus :
L = ½ a x t
dimana L adalah luas, a adalah panjang alas dan t adalah tinggi dari segitiga tersebut.
Contoh soal segitiga sama kaki dan pembahasannya
1. Jika di ketahui sebuah segitiga sama kaki panjang alasnya 12 cm sedangkan panjang kakinya 10 cm. Hitunglah luas dan keliling segitiga tersebut !
Jawab :
Diketahui :
a = 12 cm
s = 10 cm
ditanya :
a. K . . . . ?
b. L . . . . ?
Jawab :
a. Keliling segitiga
K= sisi 1 + sisi 2 + sisi 3
K = 12 cm+ 10 cm + 10 cm
K = 32 cm
b. Luas segitiga
Coba kamu perhatikan gambar segitiga segitiga sama kaki di bawah ini.

aC adalah tinggi segitiga, untuk mencari tinggi sebuah segitiga siku-siku kita bisa menggunakan persamaan phytagoras. Jika alasnya adalah 12 cm maka panjang aB = 6 cm
aC2 = BC2 - aB2
aC2 = 102 – 62
aC2 = 100 – 36
aC2 = 64
aC = 8 cm
jadi tinggi segitiga tersebut = 8 cm
Luas segitiga = ½ x a x t
L = ½ x 12 x 8
L = 48 cm2
Jadi keliling segitiga sama kaki tersebut 32 cm sedangkan luanya 48 cm2.
2. Jika diketahui luas segitiga 48 cm2. Hitung tinggi segitiga jika alasnya 12 cm !
Diketahui :
L = 48 cm2
a = 12 cm
ditanya :
t . . . . ?
jawab :
L = ½ x a x t
48 = ½ x 12 x t
48/0,5 = 12 x t
96 = 12 x t
96/12 = t
8 cm = t
Jadi tinggi segitiga tersebut 8 cm.
Rumus Segitiga Sama Sisi
Pengertian segitiga sama sisi
 Rumus Segitiga Sama Sisi - Segitiga sama sisi merupakan salah satu jenis segitiga yang dilihat dari panjang sisinya, dinamakan segitiga sama sisi di karenakan ketiga sisinya sama panjang.
Rumus Segitiga Sama Sisi - Segitiga sama sisi merupakan salah satu jenis segitiga yang dilihat dari panjang sisinya, dinamakan segitiga sama sisi di karenakan ketiga sisinya sama panjang.
Gambar di atas merupakan gambar segitiga XYZ yang panjang ketiga sisinya sama.
Segitiga sama sisi mempunyai sifat-sifat :
1. Memiliki tiga buah sisi yang sama panjang.
2. Memiliki tiga buah sudut yang sama besar.
3. Memiliki tiga buah sumbu simetri.
Nah pada segitiga sama sisi untuk menghitung luasnya selain menggunakan rumus diatas juga bisa menggunakan rumus cepat untuk mencari luasnya yaitu :
L = a2/4 x √3
dimana a merupakan panjang sisi segitiga.
Rumusnya yaitu : K = sisi 1 + sisi 2 +sisi 3
Atau bisa juga dengan cara K = panjang sisi x 3
hal tersebut bisa terjadi karena panjang semua sisinya sama.
Demikian pembahasan mengenai jenis-jenis segitiga, sifat-sifat segitiga, dan rumus-rumus segitiga. Jika masih ada pertanyaan atau materi yang kurang jelas jangan sungkan untuk bertanya melalui kolom komentar di bawah postingan ini. Semoga berhasil semuanya. Salam sukses!

Gambar di atas merupakan gambar segitiga XYZ yang panjang ketiga sisinya sama.
Segitiga sama sisi mempunyai sifat-sifat :
1. Memiliki tiga buah sisi yang sama panjang.
2. Memiliki tiga buah sudut yang sama besar.
3. Memiliki tiga buah sumbu simetri.
Rumus luas segitiga sama sisi :
Kita mengetahui jika rumus umum dari sebuah segitiga adalah L = ½ a x tNah pada segitiga sama sisi untuk menghitung luasnya selain menggunakan rumus diatas juga bisa menggunakan rumus cepat untuk mencari luasnya yaitu :
L = a2/4 x √3
dimana a merupakan panjang sisi segitiga.
Rumus keliling segitiga sama sisi :
Untuk menghitung kelilingnya saya rasa tidak ada perbedaan dengan menghitung keliling sebuah segitiga pada umumnya.Rumusnya yaitu : K = sisi 1 + sisi 2 +sisi 3
Atau bisa juga dengan cara K = panjang sisi x 3
hal tersebut bisa terjadi karena panjang semua sisinya sama.
Demikian pembahasan mengenai jenis-jenis segitiga, sifat-sifat segitiga, dan rumus-rumus segitiga. Jika masih ada pertanyaan atau materi yang kurang jelas jangan sungkan untuk bertanya melalui kolom komentar di bawah postingan ini. Semoga berhasil semuanya. Salam sukses!






0 Response to "Rumus Segitiga : Mengenal Jenis Segitiga dan Rumusnya"
Post a Comment
Manfaatkan kotak komentar di bawah ini untuk feed back dan sumbang saran. Terima kasih sudah ikut berkontribusi di blog Matematrick.